
One mathematician’s spirited answer to bored, frustrated and reluctant math students.
Eduardo Sáenz de Cabezón suspects that when people ask him what’s the use of math, they’re really asking a more pointed question. “They’re asking you, ‘Why did I have to study that bullshit I never used in my life again?’” he says. Sáenz de Cabezón (TED Talk: Math is forever) sympathizes, but as a mathematics professor at the University of La Rioja in northeastern Spain, he has come up with a spirited defense of his chosen profession. Math, he believes, is nothing less than a quest for eternal truth. Here’s why:
Math reveals unfathomable truths. Take a regular sheet of paper and start folding. If the piece of paper were big enough to be folded 50 times, Sáenz de Cabezón says, “its thickness would extend almost the distance from the Earth to the Sun.” If you’re now trying to imagine how a sheet of paper, folded 50 times, can rise nearly 93 million miles into space, you’re experiencing the strange thrill of a mathematical proof. “Your intuition tells you it’s impossible,” he says. “Do the math and you’ll see it’s right. That’s what math is for.”
Hexagons! Why they’re excellent. Anyone can posit a theory of how the universe works, but math leaves no room for conjecture. Consider how long mathematicians puzzled over a proposal by Pappus of Alexandria, who theorized in around 300 A.D. that a hexagon was surely the most efficient shape for covering an infinite flat field. “But he didn’t prove it,” says Sáenz de Cabezón. “It remained a conjecture: ‘Hexagons!’” The debate raged for 1,700 years, until in 1999 American mathematician Thomas Hales offered decisive proof of what Pappus had discovered and what bees instinctively know — the most efficient shape is indeed a hexagon. “We mathematicians devote ourselves to coming up with theorems,” says Sáenz de Cabezón. These, in essence, are “eternal truths,” discoveries that are possibly the most enduring things we will ever encounter in our lifetimes. ”You probably said or were told at some point that diamonds are forever,” Sáenz de Cabezón says. “That depends on your definition of forever. A theorem? That really is forever.”
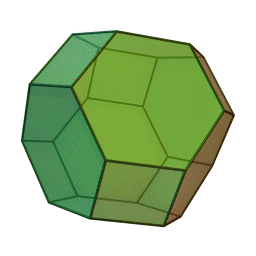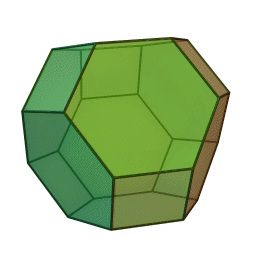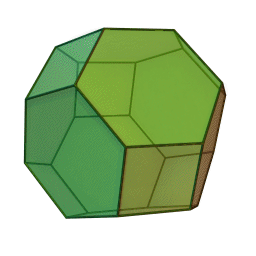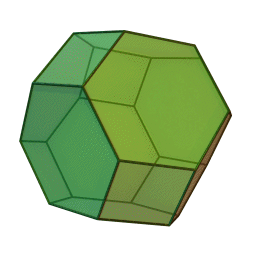
Why it turns out truncated octahedrons aren’t great after all. In 1887, Lord Kelvin, he of the Kelvin temperature scale, suggested that to cover a three-dimensional field most efficiently, you should use the 14-faced truncated octahedron. But he didn’t prove it … In 1993, Trinity College Dublin physicists Dennis Weaire and Robert Phelan discovered a different combination featuring a structure they named after themselves. “It looks like a strange object,” admits Sáenz de Cabezón, but until someone comes up with a better idea, it’s the best the mathematicians have got.
Why mathematicians find math thrilling. “Science operates on intuition, creativity. Math controls intuition and tames creativity,” says Sáenz de Cabezón. He admits that his colleagues fall into two camps when they’re asked why math matters: attackers and defenders. “The attacking ones are mathematicians who would tell you this question makes no sense, because mathematics have a meaning all their own,” Sáenz de Cabezón says. “There’s no point in constantly searching for all possible applications. What’s the use of poetry? What’s the use of love? What’s the use of life itself?” They have a point, he says — and so do the defenders. “Those who stand in defense tell you, ‘Even if you don’t realize it, friend, math is behind everything.’ Those guys, they always bring up bridges and computers. ‘If you don’t know math, your bridge will collapse.’” Also true. But Sáenz de Cabezón suspects that neither answer conveys the private thrill that mathematicians experience with every breakthrough in their field — and every push to help us better understand the world.
Featured photo: iStock.













