
Who knew equations and graphs could guide your love life? Mathematician Hannah Fry does — and shares a few formulas for finding The One.
When it comes to love, making long-term decisions is a risky business. Sooner or later, most of us decide to leave our carefree bachelor or bachelorette days behind us and settle down. Our wild oats have been sown, and it’s time for a lifelong partnership. But how do we know when we’ve truly found “The One”? As any mathematically minded person will tell you, it’s a fine balance between having the patience to wait for the right person and the foresight to cash in before all the good ones are taken. Just ask anyone who has found themselves stung by the eligible bachelor paradox.
If you decided never to settle down, you could sit back at the end of your life and list everyone you ever dated, with the luxury of being able to score each one on how good they could have been as your life partner. Such a list would be pretty pointless by then, but if only you could have it earlier, it would make choosing a life partner a fair sight easier. But the big question is, how can you select the best person on your imaginary list to settle down with, without knowing any of the information that lies ahead of you?
Spend a bit of time playing the field when you’re young, rejecting everyone you meet until you’ve got a feel for the marketplace.
Let’s assume the rules of dating are simple: Once you decide to settle down and take yourself out of the dating game, you can’t look ahead to see all the partners you could have had on your list, but equally, once you reject someone, you can’t go back and change your mind at a later date. That’s been my experience, anyway: People seem surprisingly averse to being called up several years after being rejected because no one better came along.
When dating is framed in this way, an area of mathematics called optimal stopping theory can offer the best possible strategy in your hunt for The One. And the conclusion is surprisingly sensible: Spend a bit of time playing the field when you’re young, rejecting everyone you meet as serious life-partner material until you’ve got a feel for the marketplace. Then, once that phase has passed, pick the next person who comes along who’s better than everyone you met before.
But optimal stopping theory goes further. Because it turns out your probability of stopping and settling down with the best person (denoted by P in the equation below) is linked to how many of your potential lovers (n) you reject (r), by a rather elegant formula:
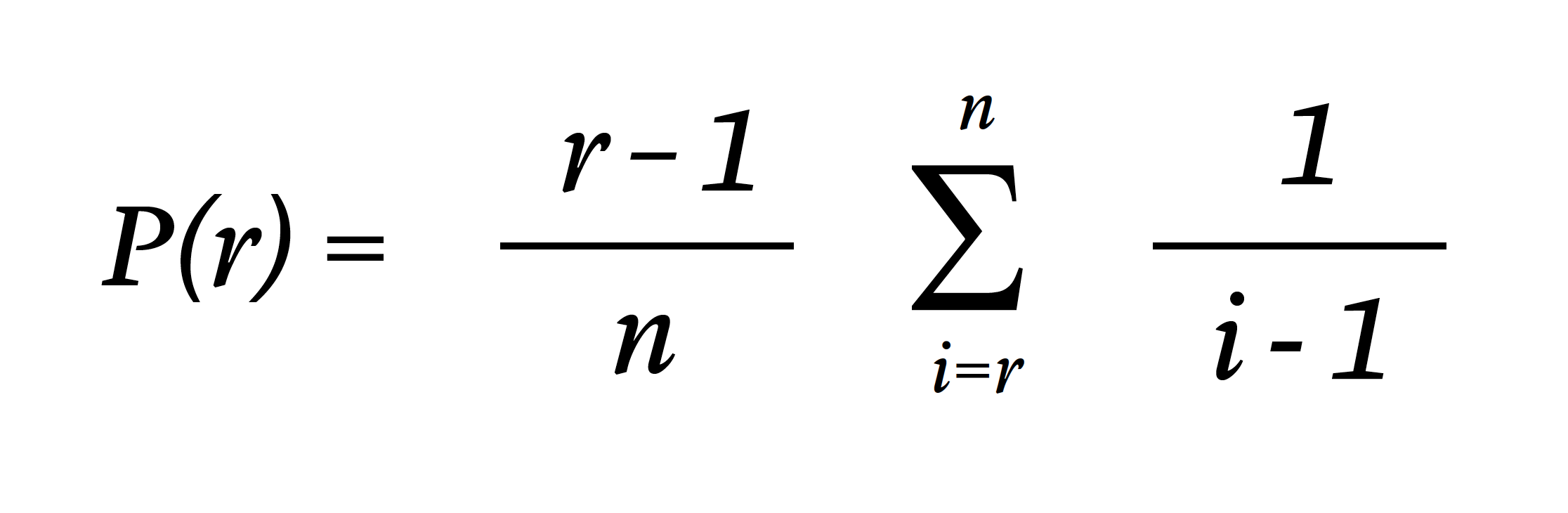
This formula has the power to tell you exactly how many people to reject to give you the best possible chance of finding your perfect partner. It tells you that if you are destined to date ten people in your lifetime, you have the highest probability of finding The One when you reject your first four lovers (where you’d find them 39.87 percent of the time). If you are destined to date 20 people, you should reject the first eight (where Mister or Miz Right would be waiting for you 38.42 percent of the time). And, if you are destined to date an infinite number of partners, you should reject the first 37 percent, giving you just over a one in three chance of success.
I’m a mathematician and therefore biased, but this result literally blows my mind. If you chose not to follow this strategy and instead opted to settle down with a partner at random, you’d only have a 1/n chance of finding your true love, or just 5 percent if you are fated to date 20 people in your lifetime, for example. But by rejecting the first 37 percent of your lovers and following this strategy, you can dramatically change your fortunes, to a whopping 38.42 percent for a destiny with 20 potential lovers.
Okay, you may have spotted flaws in this plan. Unless you’re a member of the English royal family in the 1500s, your potential dates won’t be lined up ahead of time, and there’s no way you could possibly know how many people will be available to you in your lifetime. You’re probably not going to date an infinite number of people, either.
Have three months to find a place to live? Reject everything in the first month and then pick the next house that is your favorite so far.
Thankfully, there is a second version of this problem that is much more suited to mere mortals, and it’s got an equally impressive result. Instead of knowing how many people you’ll date, the advanced problem only requires you to know how long you expect your dating life to be. The math is much trickier, though the same simple rule as earlier crops up again — but this time, the 37 percent applies to time rather than people.
Say you start dating when you are 15 years old and would ideally like to settle down by the time you’re 40. In the first 37 percent of your dating window (until just after your 24th birthday), you should reject everyone — use this time to get a feel for the market and a realistic expectation of what you can expect in a life partner. Once the rejection phase has passed, pick the next person who comes along who is better than everyone who you have met before. Following this strategy will definitely give you the best possible chance of finding the number one partner on your imaginary list. But, a warning: Even this version has its flaws.
Imagine that during your 37-percent-rejection phase you start dating someone who is your perfect partner in every possible way. But, not yet having met everyone, you’d have no way of knowing that they were the best of your list and you’d let them go. Unfortunately, once you started looking more seriously for a life partner, no one better would ever come along. According to the rules, you should continue to reject everyone else for the rest of your life, grow old and die alone, probably nursing a deep hatred of mathematical formulas. Likewise, imagine you were unlucky and everyone you met in your first 37 percent was dull and boring. You’d be in your rejection phase, and so wouldn’t end up spending a lifetime with them. Now imagine that the next person you dated was just marginally less terrible than those before. If you were still following the math, sadly, you’d marry them and find yourself trapped in a suboptimal marriage.
Beyond choosing a partner, this strategy also applies to a host of other situations where people are searching for something and want to know the best time to stop looking. Have three months to find somewhere to live? Reject everything in the first month and then pick the next house that comes along that is your favorite so far. Hiring an assistant? Reject the first 37 percent of candidates and then give the job to the next one who you prefer above all others. In fact, the search for an assistant is the most famous formulation of this theory, and the method is often known as the “secretary problem.”
If you’d be happy with anyone in the top 15 percent, you only need to spend 19 percent of your dating life finding what’s out there.
I may have oversold this “reject 37 percent” strategy in the context of dating, because the math assumes you’re only interested in finding the very best possible partner available to you. But the situation changes slightly if you’re a bit more relaxed about who you end up with. In reality, many of us would prefer a good partner to being alone if The One is unavailable. What if you would be happy with someone who was within the top 5 percent or 15 percent of your potential partners rather than insisting on all or nothing?
Mathematics can still offer answers. We can use a trick known as a Monte Carlo simulation. The idea is to set up a sort of mathematical Groundhog Day within a computer program, allowing you to simulate tens of thousands of different lifetimes, each with randomly appearing partners of random levels of compatibility. The program can experiment with what happens in each lifetime if they use a different rejection phase from the 37 percent outlined above. At the end of each simulated lifetime and with the benefit of hindsight, the program looks back at all the partners it could have had and works out if the strategy has been successful.
If you repeat this process for every possible rejection phase, for each of the three criteria of success (best partner only, someone in the top 5 percent, someone in the top fifteen percent, you end up with a graph that looks like this:
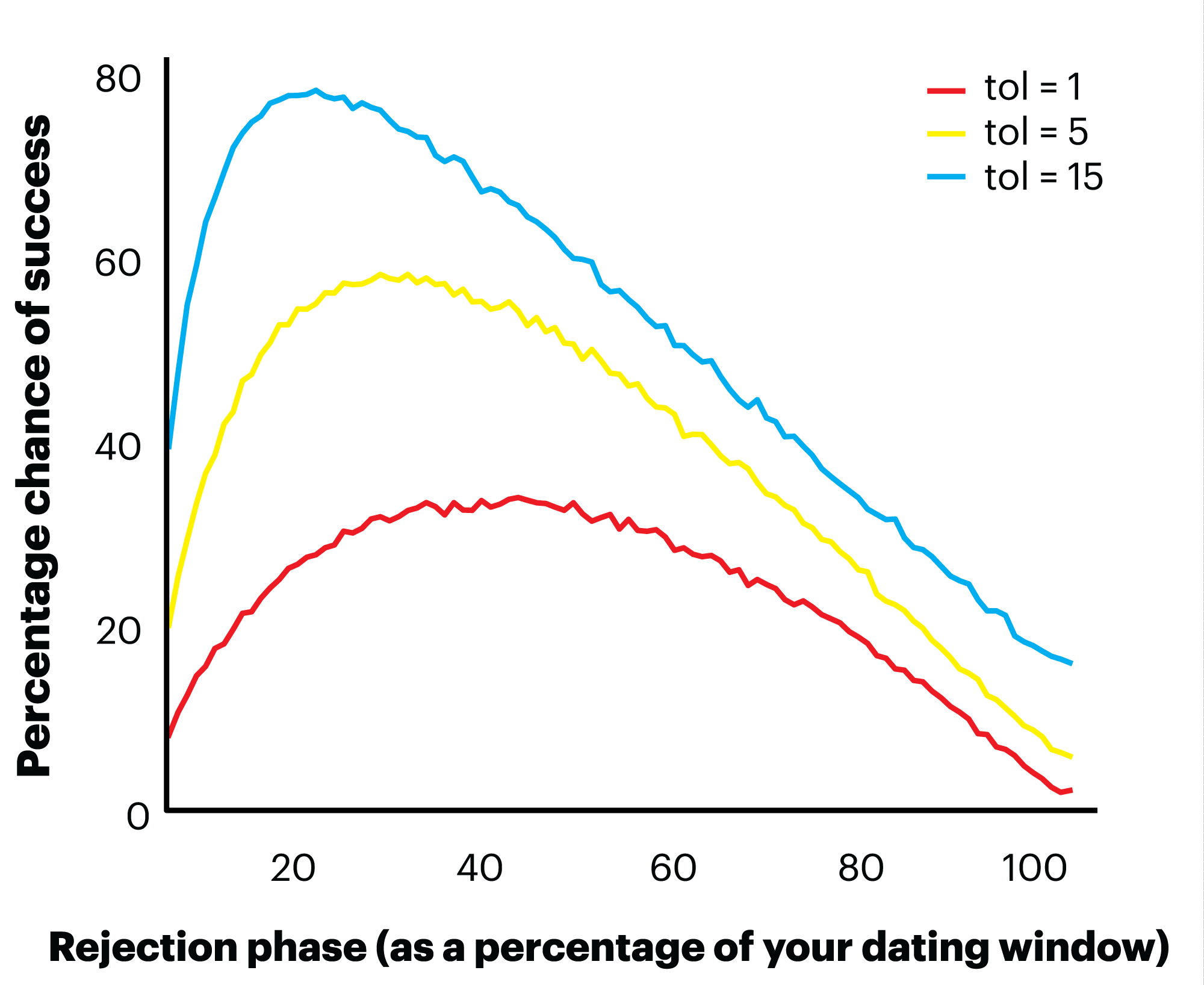
The red line is our original problem. Here, the highest possible chance of success comes with a rejection window of 37 percent as the math predicted, also giving you a 37 percent chance of settling down with the perfect partner.
But if the criteria are relaxed and you’d be happy to settle down with someone in the top 5 percent of everyone you will date in your lifetime, it’s the yellow line you need. Here, you have your best chance of success if you reject partners who appear in the first 22 percent of your dating window and pick the next person that comes along who’s better than anyone you’ve met before. Follow this strategy and you’ll settle with someone within the top 5 percent of your potential partners an impressive 57 percent of the time.
And if you would be happy with anyone in the top 15 percent, you only need to spend a mere 19 percent of your dating life getting a feel for what’s out there, as in the blue line. Use this strategy and you can expect a whopping 78 percent chance of success — much less risky than the traditional all-or-nothing version of this problem.
These ideas still aren’t perfect. Life partners aren’t like houses or assistants, which are yours if you can afford them. But nonetheless, I think this neat and simple problem offers some nice insight into the real-world scenario, even if you can’t totally take it at face value. After all, that’s what mathematics is about — abstracting from the real world to help uncover some of the hidden patterns and relationships which otherwise would be shrouded in messy things like emotions.
Excerpted with permission from the book The Mathematics of Love: Patterns, Proofs, and the Search for the Ultimate Equation, by Hannah Fry, published by TED Books/Simon & Schuster. © 2015 Dr. Hannah Fry.












